Optimizing Transition Conditions for Efficient Automaton Representation

Building a regular expression manipulation engine requires effective handling and efficient storage of finite state automata. An automaton can be visualized as a directed graph where nodes represent states and edges correspond to transition conditions. The study of graph representation and manipulation is well-established, with numerous optimized techniques available. In this article, we focus on optimizing how transition conditions are represented.

Effectively representing these transition conditions is crucial for minimizing complexity and improving performance, particularly when dealing with operations such as intersection, union, complement, and determinization of automata.

A basic approach would involve representing a condition as a set of values. However, this can quickly become impractical for large sets, like when dealing with the '.' operator in a regular expression, which matches all possible characters.

An alternative method is to use interval ranges (which I presented in a previous article). This approach reduces memory requirements by storing only the bounds of value ranges rather than each individual value. While efficient for many tasks, interval-based operations still have a complexity of O(n), where n is the number of bounds. This can become costly, particularly when dealing with the determinization of complex automata with numerous transitions.

To overcome these limitations, I developed a new approach inspired by linear algebra. This method offers O(1) complexity for all operations while maintaining minimal memory usage.

The Idea: A Minimal Basis for Transition Conditions

The key idea is to treat all transition conditions in the automaton as elements that can be expressed using a minimal basis. By computing a minimal set of base conditions that can generate any possible transition condition, we can represent each transition efficiently. In order to also represent the complement of any condition of the automaton, we add an additional basis element that represents the complement of the union of all the conditions.

For every transition condition, we store a bit-encoded representation that indicates which elements of this basis are present in the condition. Each bit in this representation corresponds to an element of the basis, allowing for extremely fast set operations, like union, intersection, and complement, using bitwise operations.

Example: Representing Transitions Using a Minimal Basis

The regular expression ([a-c][d-f]|[a-f][a-cg-i]) as an automaton

We have an automaton that needs to represent several different character classes as transition conditions. Those transition conditions are [a-c], [d-f], [a-f] and [a-cg-i]. Instead of representing each character individually, we first compute a minimal set of base conditions:

Basis Elements:

• [a-c]
• [d-f]
• [g-i]
• [^a-i] (representing all characters not in the other elements of the basis)

These form our minimal basis, which can be used to represent any transition condition in the automaton. Now, suppose we want to represent a transition condition that matches [a-cg-i]. We can use a bit vector where each bit corresponds to one of the basis elements:

Bit Representation:

• Basis: [[a-c], [d-f], [g-i], [^a-i]]
• Condition: [a-cg-i] -> Bit Vector: 1010

In this bit vector, the first and third bits are set to 1, indicating that the transition condition includes the first and third elements of the basis ([a-c] and [g-i]).

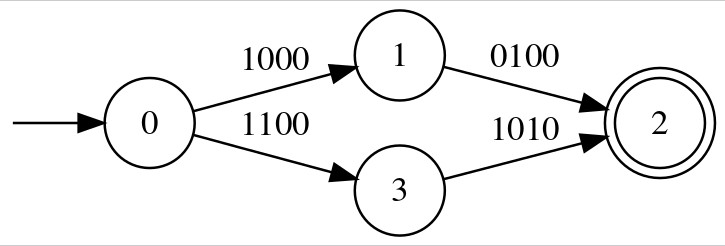The same automaton with the basis representation

With this representation, we can now perform operations like union, intersection, and complement using simple bitwise operations. For example:

• Union: To compute the union of [a-c] and [d-f], we simply take the bitwise OR of 1000 (representing [a-c]) and 0100 (representing [d-f]), resulting in 1100 (representing [a-f]).
• Intersection: To compute the intersection of [a-cg-i] (1010) with [d-i] (0110), we take the bitwise AND, resulting in 0010 (which corresponds to [g-i]).
• Complement: To compute the complement of [a-cg-i] (1010), we simply flip all the bits, resulting in 0101. This indicates that the complement includes [^a-cg-i].

This minimal basis approach allows us to represent complex transition conditions compactly and perform set operations with constant-time complexity, making it highly efficient for complex automata operations.

This method ensures that our automaton representation is both space-efficient and computationally efficient, making it well-suited for complex regex operations that require frequent manipulation of transition conditions.

Conclusion

The proposed minimal basis representation for transition conditions in finite state automata offers a highly efficient way to handle complex regex operations. By leveraging bit-encoded conditions, we can achieve constant-time operations for union, intersection, and complement, resulting in both space and computational efficiency.

This approach not only benefits automata manipulation but also proves effective in machine learning, where compact, efficient representations reduce model complexity and training time. It enhances generalization by allowing multiple automata to share identical representations with different underlying basis, reducing redundancy while ensuring consistency.

This approach has allowed me to achieve unrivaled performances on my project RegexSolver, a tool designed to manipulate regular expressions as if they were sets.